01 - Getting and Cleaning Census Data¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Dealing with the os library for basic functions
Standarizing names in Spanish with the unidecode library.

Project¶

Extract the population estimates for each municipality.
Clean the name of the municipalities in the census dataset.

Census Data¶

The United States established in 1840 a central office to oversee the census of the population of its states and territories. This office today is known as the United States Census Bureau. They perform a decenial census, the last one being in 2010. With this information they produce what is called PEPANNRES - Annual Estimates of the Resident Population in which they do population estimates by different geographic levels. In March 2018 they published the estimates for municipalities in the year 2017. This is exactly what we need for our analysis.

Getting the Data¶

The Census Bureau makes their data available through many pages and API's. Here we are going to use the FactFinder webpage and download the data manually, but it is worth noting that there are API wrappers in Python such as:

Census - https://github.com/datamade/census
Census Areas - https://github.com/datamade/census_area

If you want to get the data manually it is available in the following LINK. However, it is included as a zip file in the repository for reproducibility purposes.

Let's code!¶

Load the libraries¶

pandas is a library to do data wrangling and dealing with data in general.
os is a library that allows us to interact with the computer in a lower level than python.
unidecode is a library that helps us deal with the names of the municipalities in Spanish. (Remember, PR is a Spanish speaking nation :D)

import pandas as pd
import os
import unidecode

Extract the data¶

The data is stored in a compressed form, we need to extract it and save it in a place where we can use it.

Steps:

Extract the data ---- unzip command
Store it the data/ folder ---- -d data/ command

os.system("unzip ../data/PEP_2017_PEPANNRES.zip -d ../data/")

0

Load the data¶

pd.read_csv is a function from the pandas package that allows us to load Comma Separated Values (CSV) files into Python with ease. The head() method let's us see the top rows of the data frame.

data = pd.read_csv("../data/PEP_2017_PEPANNRES.csv", encoding='latin-1')
data.head()

Dealing with names in Spanish¶

Spanish is a beautiful language, however, when dealing with names when programming, sometimes it's hard given some inconsistencies. This comes because of a wrong encoding of the files, typing some of the names in English and some in Spanish, or simply skiping 'weird' characters. To deal with this inconsistencies, we convert the names to their english-letter representation and to an upper case. This way we standarize all the names for all the files.

Steps:

Extract the names of the municipalities from the strings
Convert the names to english-letter representation
Convert the strings to upper case format

municipalities = []

for i in range(0, 78):
    muni_raw = data['GEO.display-label'][i].split(" Municipio, Puerto Rico")[0]
    muni_clean = unidecode.unidecode(muni_raw)
    muni_upper = muni_clean.upper()
    municipalities.append(muni_upper)

data['ResidencePlace'] = municipalities

data_processed = data[['ResidencePlace', 'respop72017']]
data_processed.head()

Save the progress | Clean our directories¶

Let's save the population estimates for 2017 to use the file later in our pipeline

data_processed.to_csv("../data/census.csv")

Finally, clean the data directory to only remain with the files we need to reproduce this analysis and produce it's output.

os.system("rm ../data/PEP_2017_PEPANNRES.csv ../data/PEP_2017_PEPANNRES_metadata.csv ../data/PEP_2017_PEPANNRES.txt ../data/aff_download_readme.txt")

0

Optional Questions¶

1) What is the municipality with the highest population? How about the least?

2) Which municipality changed the most between 2016 and 2017?

3) How about between 2010 and 2017?

4) Can you find the municipality that has stayed the most stable (less variability) between all these years?

5) Are there some municipalities consistingly losing people and other winning them?

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

02 - Getting and Cleaning Mortality Data¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Use of pandas group_by function.
Filtering data with string content.

Project¶

Compute the number of deaths per zone of each municipality.
Clean the name of the municipalities in the mortality dataset.

Mortality Data¶

Hurricane Maria struck Puerto Rico the 20th of September of 2017 at 6:15 a.m. entering through the municipality of Yabucoa as a Category 4 hurricane. According to the governments of Puerto Rico and the U.S. Virgin islands, the cost of the damage is estimated in $102 billion USD1. However, the impact wasn't only economical. Following a lawsuit presented by the Center for Investigative Journalism (CPI, by its spanish initials) and CNN, the Government of Puerto Rico, and more specifically the Demographic Registry, was forced to publish the individual-level data of all the deaths occurred from September 20, 2017 to June 11, 2018. This data is available in the following Dropbox Link from the CPI.

Let's code!¶

Load the libraries¶

import pandas as pd
import os

Here we are downloading the data directly from Dropbox and storing it under the data/ folder in the mortality.xlsx file.

os.system("wget --output-document='../data/mortality.xlsx' 'https://www.dropbox.com/s/k4wrb1ztwu0fwxh/Base%20de%20Datos%20Mortalidad%20en%20PR%20de%20septiembre%2018%20de%202017%20a%2011%20de%20junio%20de%202018%20entregada%20por%20Gobierno%20de%20PR%20al%20CPI.xls?dl=0'")

0

data = pd.read_excel("../data/mortality.xlsx")
data.head()

Filtering the data¶

We are using the ResidencePlace column as the column for the Municipality
There is people that died in Puerto Rico, but there residence place is not Puerto Rico, we want to exclude those data points from the analysis.
- data[data.ResidencePlace.str.contains('PUERTO RICO')]
We also want to exclude those people we don't know their municipality of residence.
- data[data.ResidenceZone != 'DESCONOCIDO']

data = data[data.ResidencePlace.str.contains('PUERTO RICO')]
data = data[data.ResidencePlace != 'PUERTO RICO, DESCONOCIDO']
data = data[data.ResidenceZone != 'DESCONOCIDO']

Grouping the data¶

We want to compute the number of deaths in each zone of each municipality:

Group by ResidencePlace and ResidenceZone
- data.groupby(['ResidencePlace', 'ResidenceZone'])
Calculate the number of deaths per zone of each municipality
- data.groupby(['ResidencePlace', 'ResidenceZone']).size().reset_index(name='Deaths')

df_grp = data.groupby(['ResidencePlace', 'ResidenceZone']).size().reset_index(name='Deaths')
df_grp.head()

Extract the name of the municipalities from the `ResidencePlace` column¶

municipalities = df_grp.ResidencePlace.tolist()

for i in range(0,len(municipalities)):
    municipalities[i] = municipalities[i].split("PUERTO RICO, ")[1]

df_grp.ResidencePlace = pd.Series(municipalities)
df_grp.head()

Save our DataFrame as a CSV for future analysis¶

df_grp.to_csv("../data/mortality_grouped.csv")

Optional Questions¶

1) Did more women died or men?

2) Which month had the higher mortality?

3) Which was the average age of death? Did more infants died or older people?

4) Do you see any patterns in years of education?

5) Do you notice any patter in the ResidencePlace vs the Death Registry municipality? Why is this?

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

03 - Mapping Mortality Rates¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Handling of Spatial Data in Python with geopandas
Visualizing Spatial Data
Joining data from different sources

Project¶

Visualize the spatial distribution of the mortality rates
Analyze spatial patterns in the data

Let's code¶

Load the libraries¶

Here we see the %matplotlib inline command, this tells the matplotlib package to display the plots in this notebook.
We are seeing as well the geopandas library for the first time. This is a very useful library to handle spatial data in Python.

%matplotlib inline
import matplotlib.pyplot as plt
import geopandas as gpd
import pandas as pd
import numpy as np
import unidecode
import os

Get the data¶

We are downloading a GeoJSON file, which is a text file formatted to contain spatial information by hierarchies.
- Hierarchies can vary but it goes from the world, to a region, to a country, to a municipality, etc.
This GeoJSON is available from Miguel Rios GitHub repository.

os.system("wget 'https://raw.githubusercontent.com/miguelrios/atlaspr/master/geotiles/pueblos.json'")
os.system("mv 'pueblos.json' '../data/'")

0

geo_muni = gpd.read_file('../data/pueblos.json')
geo_muni.head()

On the geometry column we see a POLYGON object which is a spatial object that defines the boundary coordinates of the municipalities.

Plot the municipalities¶

Calling the GeoDataFrame by its name with the .plot() object, will plot the geometry column which in this case is our polygons of the municipalities

geo_muni.plot()

<matplotlib.axes._subplots.AxesSubplot at 0x7fc0e4039cf8>

Cleaning the municipalities name¶

This is the same procedure as in notebook_01.

municipalities = []

for i in range(0, 78):
    muni_raw = geo_muni['NAME'][i].split(" Municipio, Puerto Rico")[0]
    muni_clean = unidecode.unidecode(muni_raw)
    muni_upper = muni_clean.upper()
    municipalities.append(muni_upper)
    
geo_muni['NAME'] = municipalities

Loading Census Data¶

census_data = pd.read_csv("../data/census.csv")
census_data = census_data.drop(['Unnamed: 0'], axis = 1)
census_data.head()

Loading Mortality Data¶

mortality_data = pd.read_csv("../data/mortality_grouped.csv")
mortality_data = mortality_data.drop(['Unnamed: 0'], axis = 1)
mortality_data.head()

Calculating mortality rates¶

We first join the census data to the mortality DataFrame. This order matters as the mortality DataFrame has more information than the census data.
We then divide the number of deaths by the number of people in each municipality and the multiply by 1000 to get the mortality rate per 1000 people.

df = mortality_data.merge(census_data, on='ResidencePlace')
df['death_rate'] = (df['Deaths']/df['respop72017']) * 1000
df.head()

Join the mortality data and the spatial data¶

geo_muni['death_rate'] = list(df.groupby(['ResidencePlace'])['death_rate'].sum())

Let's plot the death rate by municipality and compare it with the trajectory of the hurricane¶

figure, ax = plt.subplots(1)

geo_muni.plot(column = 'death_rate', 
              scheme = 'quantiles', 
              legend = True, 
              ax = ax,
              edgecolor='1', 
              linewidth = 0.3)

fig = plt.gcf()
fig.set_size_inches(7, 6)
fig.set_dpi(125)
plt.title("Mortality rate per 1,000 individuals\n Timeframe from September 20, 2017 to June 2018")
ax.set_axis_off()

plt.axis('equal')
plt.show()

Source: NYTimes

Optional Questions¶

1) Do you see a pattern between the trajectory of the Hurricane and the mortality rates' spatial distribution?

2) Do you see a difference between rural zones and urban zones? Their means? Their variances? Maybe remember the groupby function to do this step. We will go way more in depth in the next notebook.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

04 - Estimating Mortality Rates through Puerto Rico¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Getting to know the PyMC3 library
Starting to think about Bayesian methods
Think about uncertainty in the estimates instead of significance vs no-significance (*Not a fan of the p-value)

Project¶

Estimate the mortality rate for urban areas as compared to rural areas.
Identify which area needs more attention for future disasters.

Bayesian methods¶

Bayesian Paradigm¶

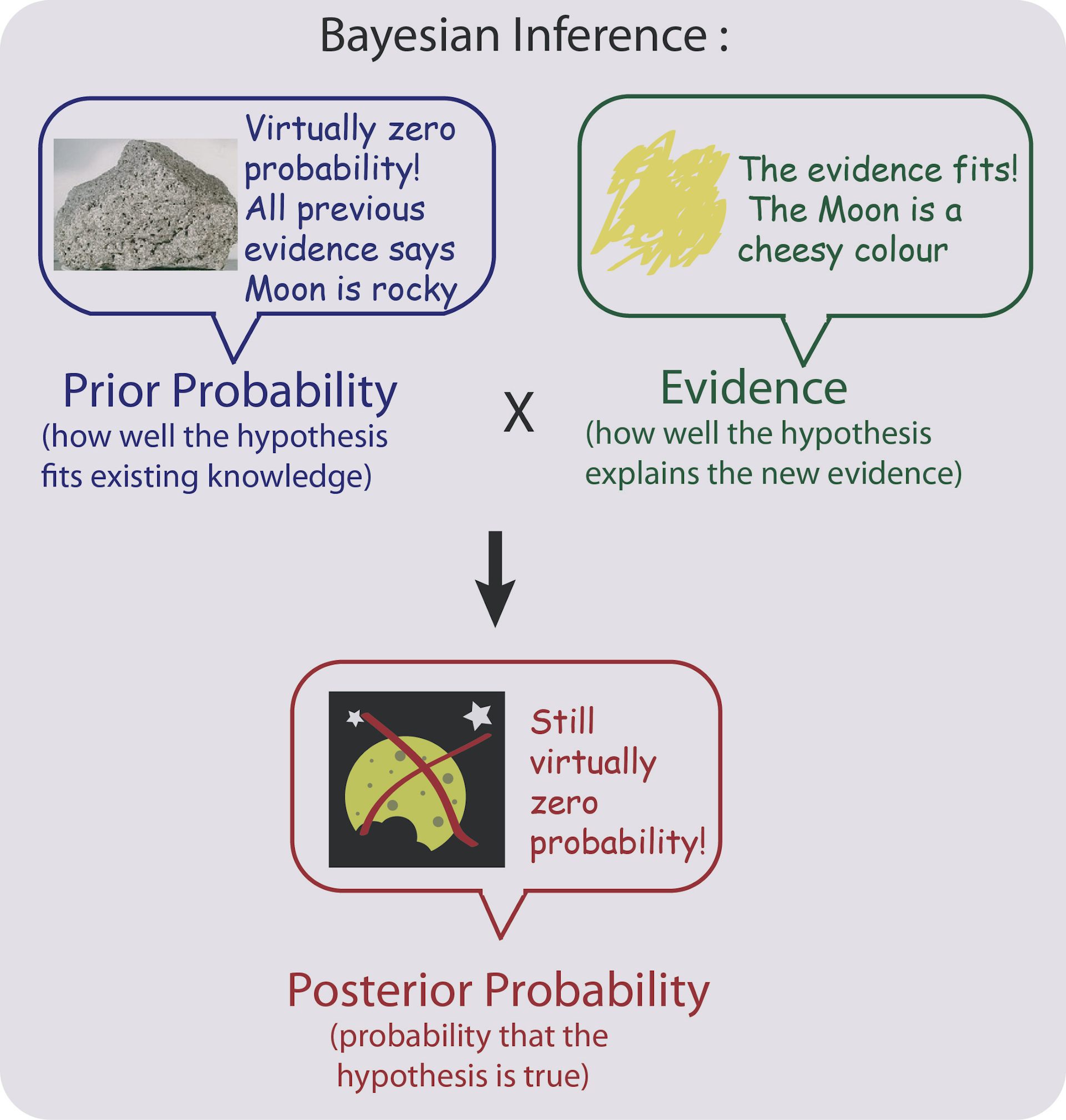
What if we have previous knowledge, or have expert knowledge regarding a certain subject that we would like to incorporate? With Bayesian methods, we can set something that is called a prior, which is a distribution for each parameter of the phenomenom we want to estimate or test. We combine this priors with the data (a.k.a Likelihood) to obtain a posterior distribution which allows us the necessary inference.

DISCLAIMER: Priors are controversial as some people have suggested that one can skew the results of the posterior distribution by setting the priors to certain values. This might be true in cases of few data points, however, in an open and reproducible science approach this should not be a concern as everyone alse can see your work. This is a big difference between using tools such as R and Python as compared to other click-and-touch software.

Source: The Conversation

History¶

Thomas Bayes discovered it.
Pierre-Simon Laplace greatly expanded the methods working with demographic data from France
- Didn't know about Bayes discovery as British-French relations at the moment weren't great, even though Laplace was almost two centuries later.
- Also invented the Central Limit Theorem, a crucial mathematical concept to understand computation bayesian methods.
- Invented the mathematical system for inductive reasoning in probability.

Uses¶

Misile production estimation
- Estimating the number of tanks the German Nazis were producing per factory
Cracking the encryption
- Breaking the Lorenz cipher using Bayesian methods
Coast Guard Searchs
- Searhing by quadrants for submarines in the Atlantic Ocean
Election Prediction

Let's code¶

Load the libraries¶

import pandas as pd
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt

/home/kropotkin/anaconda3/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
  from ._conv import register_converters as _register_converters

Load the data¶

census_data = pd.read_csv("../data/census.csv")
census_data = census_data.drop(['Unnamed: 0'], axis = 1)

mortality_data = pd.read_csv("../data/mortality_grouped.csv")
mortality_data = mortality_data.drop(['Unnamed: 0'], axis = 1)

Calculating mortality rates¶

We first join the census data to the mortality DataFrame. This order matters as the mortality DataFrame has more information than the census data.
We then divide the number of deaths by the number of people in each municipality and the multiply by 1000 to get the mortality rate per 1000 people.

df = mortality_data.merge(census_data, on='ResidencePlace')
df['death_rate'] = (df['Deaths']/df['respop72017']) * 1000
df.head()

Here we are making two DataFrames, one with the information for the rural zones and one for the urban zones.

rural = df[df['ResidenceZone'] == 'RURAL']['death_rate']
urban = df[df['ResidenceZone'] == 'URBANO']['death_rate']

PyMC3, the package we are using for Bayesian estimation, requires the data in a certain structure, which is what we are doing in this code cell below.

total = pd.DataFrame(dict(death_rate = np.r_[rural, urban],
                         group = np.r_[['rural']* len(rural), 
                                      ['urban'] * len(urban)]))
total.head()

Priors¶

As mentioned before, when doing bayesian estimation we need to set our priors. In this case I'm stating that our priors for the mean mortality rate in each zone should be close to the total death rate. In this case, I am modeling this priors with a TruncatedNormal distribution, bounded between 0 and a 1000, from the PyMC3 library. This would mean the extreme of either no one dying or everyone dying respectively. As we don't know much about the variability of the data, we model it for both zones with a Uniform distribution between 0 and 10. v is the degrees of freedom, we are centering the mean around 2 in this case with a Gamma distribution.

mu_total = total.death_rate.mean()
std_total = total.death_rate.std()

with pm.Model() as model:
    rural_mean = pm.TruncatedNormal('rural_mean', 
                                    mu = mu_total, 
                                    sd = std_total, 
                                    lower = 0, upper = 1000)
    urban_mean = pm.TruncatedNormal('urban_mean', 
                                    mu = mu_total, 
                                    sd = std_total, 
                                    lower = 0, upper = 1000)

std_low = 0
std_high = 10

with model:
    rural_std = pm.Uniform('rural_std', lower = std_low,
                          upper = std_high)
    urban_std = pm.Uniform('urban_std', lower = std_low, 
                          upper = std_high)

with model:
    v = pm.Gamma('v', alpha = 3, beta = 1)

Likelihood¶

In this code cell we are describing the final distribution, which is a StudentT distribution to compare the mean of the two groups at the end. We are passing the different arguments to the distribution and at the end with the observed argument we are feeding the model the data we have observed.

with model:
    lambda_rural = rural_std**-2
    lambda_urban = urban_std**-2
    
    rural_try = pm.StudentT('rural', nu = v, mu = rural_mean, 
                            lam = lambda_rural, observed = rural)
    urban_try = pm.StudentT('urban', nu = v, mu = urban_mean, 
                           lam = lambda_urban, observed = urban)

Here, we are calculating the differences of the resulting distributions to see if there is a difference between both zones.

with model:
    diff_of_means = pm.Deterministic('difference of means', 
                                     rural_mean - urban_mean)
    
    diff_of_stds = pm.Deterministic('difference of stds', 
                                    rural_std - urban_std)

Sampling¶

We are going to take samples from this distributions, in our case it will be 20,000 samples, over 4 cores, discarding the first 15,000 samples in each chain. This leaves us with a total of 140,000 samples from the distributions.

with model:
    trace = pm.sample(20000, cores = 4, tune = 15000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, urban_std, rural_std, urban_mean, rural_mean]
Sampling 4 chains: 100%|██████████| 140000/140000 [01:21<00:00, 1714.77draws/s]

Let's look at the posterior of the mean of the mortality rate in urban zones. What do you see?

pm.plot_posterior(trace, varnames = ['urban_mean'], color = '#0d98ba')

<matplotlib.axes._subplots.AxesSubplot at 0x7fad46d4c588>

We can observe that the mean is centered around 2.142 with a 95% chance that the real number is between 1.862 and 2.429, which means that we can say that in average, for every 1000 people, 2 died in urban zones. Below we can see that the standard deviation for the urban zones is 1.063.

pm.plot_posterior(trace, varnames = ['urban_std'], color = '#0d98ba')

<matplotlib.axes._subplots.AxesSubplot at 0x7fad35509978>

Now, let's look at the posterior of the mean of the mortality rate in rural zones. Do you notice a difference?

pm.plot_posterior(trace, varnames = ['rural_mean'], color = '#0d98ba')

We can observe that the mean is centered around 4.126 with a 95% chance that the real number is between 3.81 and 4.451, which means that we can say that in average, for every 1000 people, 4 died in rural zones. Below we can see that the standard deviation for the rural zones is 1.207, which means that the variability between urban and rural zones was similar.

pm.plot_posterior(trace, varnames = ['rural_std'], color = '#0d98ba')

However, how does the rural distribution as a whole compare to the urban distribution?

pm.plot_posterior(trace, varnames = ['difference of means'], color = '#0d98ba', ref_val=0)

Above we can see that approximately, in avergae, 2 more people died in rural zones as compared to urban zones.

pm.forestplot(trace, varnames = ['rural_mean', 'urban_mean'])

<matplotlib.gridspec.GridSpec at 0x7fad35454be0>

Finally, if we compare the different chains of the sample visually we can see that they are all very diiferent between zones.

Optional Questions¶

1) Do you think this analysis could incorporate other variables? 2) How do you think the results compare to the frequentist paradigm? Do you prefer to know the uncertainty in your results or have a single number to which you can refer to? 3) I encourage you to play with the PyMC3 package more as you can do very exciting things. (Such as model the result of football games)

References¶

This work was inpired in part by this work done by the PyMC3 development team:https://docs.pymc.io/notebooks/BEST.html

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

	GEO.id	GEO.id2	GEO.display-label	rescen42010	resbase42010	respop72010	respop72011	respop72012	respop72013	respop72014	respop72015	respop72016	respop72017
0	0500000US72001	72001	Adjuntas Municipio, Puerto Rico	19483	19483	19472	19297	19116	19019	18798	18560	18276	17971
1	0500000US72003	72003	Aguada Municipio, Puerto Rico	41959	41959	41913	41532	41107	40707	40135	39539	38853	38118
2	0500000US72005	72005	Aguadilla Municipio, Puerto Rico	60949	60949	60766	59976	58978	58036	57078	55808	54525	53164
3	0500000US72007	72007	Aguas Buenas Municipio, Puerto Rico	28659	28659	28652	28333	28052	27782	27350	26913	26382	25850
4	0500000US72009	72009	Aibonito Municipio, Puerto Rico	25900	25900	25874	25537	25205	24879	24448	24040	23566	23108

	ResidencePlace	respop72017
0	ADJUNTAS	17971
1	AGUADA	38118
2	AGUADILLA	53164
3	AGUAS BUENAS	25850
4	AIBONITO	23108

	DeathNumber	Volumen	CertificateNumber	InscriptionYear	RegistryOffice	RegistrationDate	RegistrationDate_Year	RegistrationDate_Month	RegistrationDate_Day	Name	...	FuneralDate	FuneralDate_Year	FuneralDate_Month	FuneralDate_Day	DispositionName	DispositionPlace	FuneralFacilityName	FuneralFacilityLicenseNumber	FuneralFacilityPlace	FuneralFacilityDirectorName
0	20099	34	186	2017	88 - COAMO	2017-09-26	2017	9	26	GLORIA	...	2017-09-22 00:00:00	2017.0	9.0	22.0	PORTA COELI CREMATION PLUS	BAYAMON, PUERTO RICO	FUNERARIA COAMEÑA	NaN	COAMO, PUERTO RICO	DANIEL DIAZ AQUINIO
1	20147	34	1286	2017	44 - BAYAMON	2017-10-03	2017	10	3	MARISOL	...	2017-09-30 00:00:00	2017.0	9.0	30.0	MONTE CALVARIO	CAGUAS, PUERTO RICO	FUNERARIA ALTERNATIVE	NaN	BAYAMON, PUERTO RICO	HECTOR COLON
2	20160	34	1085	2017	1 - NIVEL CENTRAL	2017-10-03	2017	10	3	RAMON	...	2017-09-26 00:00:00	2017.0	9.0	26.0	MUNICIPAL NUEVO	ARECIBO, PUERTO RICO	GONZALEZ	NaN	ARECIBO, PUERTO RICO	ROLANDO VELEZ MENDEZ
3	20168	34	1089	2017	1 - NIVEL CENTRAL	2017-10-03	2017	10	3	GLORIA	...	2017-09-26 00:00:00	2017.0	9.0	26.0	NUEVO JERUSALEN	UTUADO, PUERTO RICO	UTUADO MEMORIAL	NaN	UTUADO, PUERTO RICO	OLGA SAVEDA
4	20169	34	1297	2017	44 - BAYAMON	2017-10-03	2017	10	3	LUIS	...	2017-09-30 00:00:00	2017.0	9.0	30.0	NEW HORIZONS	BAYAMON, PUERTO RICO	FUNERARIA ASENCIO	NaN	BAYAMON, PUERTO RICO	MELVIN PORTALATIN MONTALVO

	STATE	COUNTY	NAME	geometry
0	72	071	Isabela	POLYGON ((-67.10327599999999 18.513426, -67.10...
1	72	005	Aguadilla	POLYGON ((-67.10327599999999 18.513426, -67.10...
2	72	013	Arecibo	POLYGON ((-66.58677804052712 18.48494807068136...
3	72	065	Hatillo	POLYGON ((-66.76483496560731 18.48406974021553...
4	72	115	Quebradillas	POLYGON ((-66.90143020590587 18.48455227031116...

	ResidencePlace	respop72017
0	ADJUNTAS	17971
1	AGUADA	38118
2	AGUADILLA	53164
3	AGUAS BUENAS	25850
4	AIBONITO	23108

	ResidencePlace	ResidenceZone	Deaths
0	PUERTO RICO, ADJUNTAS	RURAL	63
1	PUERTO RICO, ADJUNTAS	URBANO	50
2	PUERTO RICO, AGUADA	RURAL	165
3	PUERTO RICO, AGUADA	URBANO	37
4	PUERTO RICO, AGUADILLA	RURAL	320

	death_rate	group
0	3.505648	rural
1	4.328664	rural
2	6.019111	rural
3	5.299807	rural
4	4.111130	rural

01 - Getting and Cleaning Census Data¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Project¶

Census Data¶

Getting the Data¶

Let's code!¶

Load the libraries¶

Extract the data¶

Load the data¶

Dealing with names in Spanish¶

Save the progress | Clean our directories¶

Optional Questions¶

02 - Getting and Cleaning Mortality Data¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Project¶

Mortality Data¶

Let's code!¶

Load the libraries¶

Filtering the data¶

Grouping the data¶

Extract the name of the municipalities from the ResidencePlace column¶

Save our DataFrame as a CSV for future analysis¶

Optional Questions¶

03 - Mapping Mortality Rates¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Project¶

Let's code¶

Load the libraries¶

Get the data¶

Plot the municipalities¶

Cleaning the municipalities name¶

Loading Census Data¶

Loading Mortality Data¶

Calculating mortality rates¶

Join the mortality data and the spatial data¶

Let's plot the death rate by municipality and compare it with the trajectory of the hurricane¶

Optional Questions¶

04 - Estimating Mortality Rates through Puerto Rico¶

by Ian Flores Siaca¶

October 2018¶

Purpose of this Notebook¶

Learning¶

Project¶

Bayesian methods¶

Bayesian Paradigm¶

History¶

Uses¶

Let's code¶

Load the libraries¶

Load the data¶

Calculating mortality rates¶

Priors¶

Likelihood¶

Sampling¶

Optional Questions¶

References¶

Extract the name of the municipalities from the `ResidencePlace` column¶